题目链接 zeitgeist
1. 问题描述
首先看一下问题描述:
Everybody knows that you don’t really have to use the ZK version of SNARKs, because the proofs are so small anyway and can’t reveal much. Or do you?
A few years ago, Bob signed up to SuperCoolAirdrop™. The process was simple: provide a hash of your private key to register and when your airdrop is ready you’ll receive a notification. Today, Bob finally received a notification from SuperCoolAirdrop™. It’s time to claim his airdrop! The process is simple, he just needs to give a proof of knowledge that he knows the private key associated with the commitment he made years ago. To prevent replay attacks, SuperCoolAirdrop™ implemented a nullifier system: on top of proving knowledge of the private key, users must create a secret nonce and produce a public nullifier. Once the SuperCoolAirdrop™ server verifies the proof and logs the nullifier, the proof cannot be re-used. So Bob picks a random nonce, his favorite proof system and sends in a proof. The proof gets rejected… weird. He samples a new nonce and tries again. And again. And again. Still, his proofs get rejected. Suddenly it dawns on him. Is SuperCoolAirdrop™ legit? Is this an attempt to steal his private key?
每个人都知道你实际上并不是必须去使用ZK版本的SNARKs,因为总之证明太小了,不能从里面揭露太多信息?你觉得呢?
几年前,Bob注册了SuperCoolAirdrop™。 步骤很简单:提供一个私钥的哈希去注册,当你的空投准备好的时候将收到一个提示。 今天,Bob终于获得了SuperCoolAirdrop™的提示。领取空投的时间到了! 这个步骤很简单,他只需要去获得一个他知道与他多年前生成的承诺相关联的私钥的知识的证明。 为了阻止重放攻击,SuperCoolAirdrop™ 实现一个nullifier系统:在证明私钥的知识之上,用户必须创建一个临时nonce和一个公开的nullifier。 一旦SuperCoolAirdrop™服务器验证了证明并记录nullifier,证明就不能再次使用了。 所以Bob生成了一个随机的nonce,他最爱的证明系统,并发送了证明。证明被拒绝了。。。奇怪。他生成一个新的nonce重新试。再试。再试。他的证明还是被拒绝。 他突然想到,SuperCoolAirdrop™是合法的吗?是否在尝试透他的密钥?
根据以上的描述,已知prover视线有一个私钥,一个随机的nonce,然后他要生成私钥的哈希作为承诺(Commitment),并使用私钥和nonce共同生产的哈希值,作为nullifier。 兑换空投的时候,prover要生成一个证明,去验证他的私钥,nonce与之前生成的承诺(Commitment)和nullifier相关联。
但是,如果prover多次生成随机nonce,对应的承诺(Commitment)和nullifier,及对应的证明(proof),那么问题就是,当snark的版本是不带zk性质的话,verifier是否可以根据这多个proof,破解出prover的私钥?
2. 代码原理分析
首先来看一下 main() 函数。
pub fn main() {
welcome();
puzzle(PUZZLE_DESCRIPTION);
/* This is how the serialized proofs, nullifiers and commitments were created. */
// serialize();
/* Implement your attack here, to find the index of the encrypted message */
let secret = Fr::from(0u64);
let secret_commitment = poseidon_base::primitives::Hash::<
_,
P128Pow5T3Compact<Fr>,
ConstantLength<2>,
WIDTH,
RATE,
>::init()
.hash([secret, Fr::from(0u64)]);
for i in 0..64 {
let (_, _, commitment) = from_serialized(i);
assert_eq!(secret_commitment, commitment);
}
/* End of attack */
}
serialize() 函数里面包含创建序列化的 proofs,nullifiers 和commitments 的代码。
pub fn serialize() {
for i in 0..64 {
let (proof, nullifier, commitment) = shplonk();
let filename = format!("./proofs/proof_{}.bin", i);
let mut file = File::create(&filename).unwrap();
file.write_all(&proof).unwrap();
let filename = format!("./nullifiers/nullifier_{}.bin", i);
let mut file = File::create(&filename).unwrap();
file.write_all(&nullifier.to_repr()).unwrap();
let filename = format!("./commitments/commitment_{}.bin", i);
let mut file = File::create(&filename).unwrap();
file.write_all(&commitment.to_repr()).unwrap();
}
}
pub fn shplonk() -> (Vec<u8>, Fr, Fr) {
use halo2_proofs::poly::kzg::commitment::{KZGCommitmentScheme, ParamsKZG};
use halo2_proofs::poly::kzg::multiopen::{ProverSHPLONK, VerifierSHPLONK};
use halo2_proofs::poly::kzg::strategy::AccumulatorStrategy;
use halo2curves::bn256::Bn256;
use rand_chacha::ChaCha20Rng;
use rand_core::SeedableRng;
let setup_rng = ChaCha20Rng::from_seed([1u8; 32]);
let params = ParamsKZG::<Bn256>::setup(K, setup_rng);
let rng = OsRng;
let pk = keygen::<KZGCommitmentScheme<_>>(¶ms);
let (proof, nullifier, commitment) =
create_proof::<_, ProverSHPLONK<_>, _, _, Blake2bWrite<_, _, Challenge255<_>>>(
rng, ¶ms, &pk,
);
let verifier_params = params.verifier_params();
verify_proof::<
_,
VerifierSHPLONK<_>,
_,
Blake2bRead<_, _, Challenge255<_>>,
AccumulatorStrategy<_>,
>(
verifier_params,
pk.get_vk(),
&proof[..],
nullifier,
commitment,
);
(proof, nullifier, commitment)
}
根据这部分代码可以获知,Bob使用的证明系统是Halo2,commitment方案是SHPLONK。
再来看一下电路代码。
#[derive(Default, Clone)]
struct MyCircuit {
witness: Value<Fr>,
nonce: Value<Fr>,
}
const WIDTH: usize = 3;
const RATE: usize = 2;
#[derive(Clone, Debug)]
struct MyCircuitConfig {
input_config: InputConfig,
hash_config: Pow5Config<Fr, WIDTH, RATE>,
commitment_hash_config: Pow5Config<Fr, WIDTH, RATE>,
}
impl Circuit<Fr> for MyCircuit {
type Config = MyCircuitConfig;
type FloorPlanner = SimpleFloorPlanner;
fn without_witnesses(&self) -> Self {
Self::default()
}
fn configure(meta: &mut ConstraintSystem<Fr>) -> Self::Config {
// LOAD CONFIG
let witness = meta.advice_column();
let instance = meta.instance_column();
let constant = meta.fixed_column();
let input_config = InputChip::configure(meta, witness, instance, constant);
let witness_state = (0..WIDTH).map(|_| meta.advice_column()).collect::<Vec<_>>();
let witness_partial_sbox = meta.advice_column();
let witness_rc_a = (0..WIDTH).map(|_| meta.fixed_column()).collect::<Vec<_>>();
let witness_rc_b = (0..WIDTH).map(|_| meta.fixed_column()).collect::<Vec<_>>();
meta.enable_constant(witness_rc_b[0]);
let witness_hash_config = Pow5Chip::configure::<P128Pow5T3<Fr>>(
meta,
witness_state.try_into().unwrap(),
witness_partial_sbox,
witness_rc_a.try_into().unwrap(),
witness_rc_b.try_into().unwrap(),
);
// POSEIDON CONFIG
let state = (0..WIDTH).map(|_| meta.advice_column()).collect::<Vec<_>>();
let partial_sbox = meta.advice_column();
let rc_a = (0..WIDTH).map(|_| meta.fixed_column()).collect::<Vec<_>>();
let rc_b = (0..WIDTH).map(|_| meta.fixed_column()).collect::<Vec<_>>();
meta.enable_constant(rc_b[0]);
let hash_config = Pow5Chip::configure::<P128Pow5T3<Fr>>(
meta,
state.try_into().unwrap(),
partial_sbox,
rc_a.try_into().unwrap(),
rc_b.try_into().unwrap(),
);
return Self::Config {
input_config,
hash_config,
commitment_hash_config: witness_hash_config,
};
}
fn synthesize(
&self,
config: Self::Config,
mut layouter: impl Layouter<Fr>,
) -> Result<(), Error> {
let input_chip = InputChip::<_>::construct(config.input_config);
let x = input_chip.load_witness(layouter.namespace(|| "load secret"), self.witness)?;
let nonce = input_chip.load_nonce(layouter.namespace(|| "load nonce"), self.nonce)?;
let c = input_chip.load_constant(layouter.namespace(|| "load const"), Fr::from(0u64))?;
let commitment_hash_chip = Pow5Chip::construct(config.commitment_hash_config.clone());
let commitment_hasher = Hash::<_, _, P128Pow5T3<Fr>, ConstantLength<2>, WIDTH, RATE>::init(
commitment_hash_chip,
layouter.namespace(|| "init witness"),
)?;
let commitment_digest =
commitment_hasher.hash(layouter.namespace(|| "commitment"), [x.0.clone(), c.0])?;
input_chip.expose_public(
layouter.namespace(|| "expose commitment"),
Number(commitment_digest),
1,
)?;
// START HASHING
let poseidon_chip = Pow5Chip::construct(config.hash_config.clone());
let hasher = Hash::<_, _, P128Pow5T3<Fr>, ConstantLength<2>, WIDTH, RATE>::init(
poseidon_chip,
layouter.namespace(|| "init"),
)?;
let nullifier = hasher.hash(layouter.namespace(|| "hash"), [x.0, nonce.0])?;
input_chip.expose_public(
layouter.namespace(|| "expose nullifier"),
Number(nullifier),
0,
)?;
Ok(())
}
}
prover要输入两个private inputs(也就是advices),一个是私钥,也就是secret(witness),另一个是nonce,还有两个public inputs,一个是commitment,另一个是nullifier。
电路的内容是去检查两个哈希的运算,一个是commitment = hash(secret), 另一个是 nullifier = hash(secret, nonce)。
这里有三个chip,总共有9列advice,
其中第一个chip是input_chip,用了一列的advice,就是第0列。这个chip占用了两行,排布两个值,第0行是secret, 第1行是nonce。
第二个chip是commitment_hash_chip,用了4列的advice,就是第1-4列。这个chip从第二行开始排布,共40行。并且其中第1列的前三个值就是secret。
第三个chip是poseidon_chip,用了4列的advice,就是第5-8列。跟commitment_hash_chip的结构相同,从第二行开始排布,共40行。并且其中第5列的前三个值就是secret,第6列的前三个值就是nonce。
advice其它部分为闲置的cell。
如下图是advice的排布:

3. 问题分析
在题目中,Bob(prover)重复提交了多次证明。每次私钥是相同的,但nonce不同。这里可以观察到,第1-4列的内容仅跟secret有关,而与nonce无关。所以在Bob提交的多个证明中,这四行的advice值是完全不变的。 我们知道在Plonk里面,每一列的advice都会构造成一个多项式(即图上的a(X), b(X), c(X)),

图上是带有零知识版本的协议,它使用一个混有随机数的多项式(红色框里面的内容)来使得每次生成的多项式都是不一样的。如果去掉zk的部分,那么显然,在Bob提交的多次证明中,第1-4列的多项式的是不变的。
Plonk协议接下来会取一个随机挑战值z(代码中为x)计算各个多项式在x处的取值,作为proof的一部分,最终再由verifier对各个多项式做多项式承诺的验证。

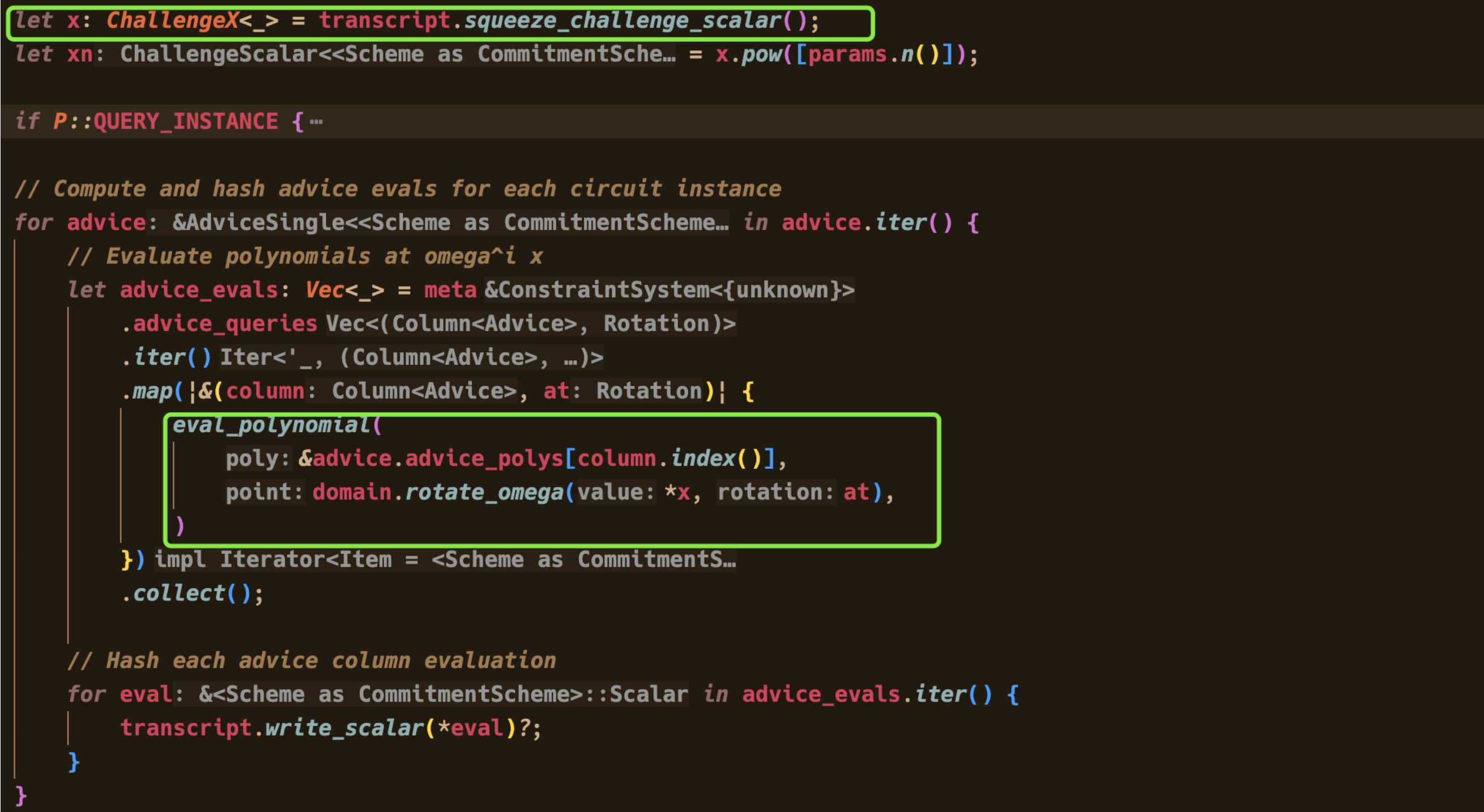
也就是说,每生成一次证明,verifier都能获得1-4列多项式在一个随机点处的取值。 这里多项式的阶数是64。也就是说,只要能获得这几列多项式在65个不同点处的取值,就可以使用拉格朗日插值的方法计算出多项式,用系数式的形式表示出来。 而我们已经发现了,在第1列的第0-1列是闲置的,值为0。而第2-4个位置的取值就是secret。
4. 解题
总结一下,Bob使用了不带zk性质的plonk证明系统。电路中使用了9列的advice,使用相同私钥(就是secret)构造的电路的第1-4列内容是完全相同的。并且第1列的第0-1位置内容为0,第2-4位置是secret。
代码仓库里面给我们提供了64组proof,commitment和nullifier。也就是说verifier从这里已经可以得到第1列多项式在64个随机点处的取值了。再加上第0位置上的取值为0,假设多项式为l(x),那么l(\omega^0) = 0。 因此利用这65个点处的取值就能通过拉格朗日插值法计算出l(x)多项式了。从而计算出secret = l(\omega^2).
pub fn main() {
welcome();
puzzle(PUZZLE_DESCRIPTION);
/* This is how the serialized proofs, nullifiers and commitments were created. */
// serialize();
/* Implement your attack here, to find the index of the encrypted message */
use halo2_proofs::poly::kzg::commitment::{KZGCommitmentScheme, ParamsKZG};
use halo2curves::bn256::Bn256;
use halo2_proofs::transcript::{Transcript, TranscriptRead};
use halo2_proofs::arithmetic::lagrange_interpolate;
use halo2curves::bn256::G1Affine;
use halo2_proofs::arithmetic::eval_polynomial;
// Generate pk/vk
let setup_rng = ChaCha20Rng::from_seed([1u8; 32]);
let params = ParamsKZG::<Bn256>::setup(K, setup_rng);
let pk = keygen::<KZGCommitmentScheme<_>>(¶ms);
let vk = pk.get_vk();
let mut points = Vec::new();
let mut evals = Vec::new();
// Read the l(x) from proof for the second column for advice
for i in 0..64 {
let (proof, nullifier, commitment) = from_serialized(i);
let mut transcript: Blake2bRead<&[u8], G1Affine, Challenge255<G1Affine>> = Blake2bRead::<&[u8], G1Affine, Challenge255<G1Affine>>::init(&proof);
vk.hash_into(&mut transcript).unwrap();
transcript.common_scalar(nullifier).unwrap();
transcript.common_scalar(commitment).unwrap();
transcript.read_point().unwrap();
transcript.read_point().unwrap();
transcript.read_point().unwrap();
transcript.read_point().unwrap();
transcript.read_point().unwrap();
transcript.read_point().unwrap();
transcript.read_point().unwrap();
transcript.read_point().unwrap();
transcript.read_point().unwrap();
transcript.squeeze_challenge_scalar::<()>();
transcript.squeeze_challenge_scalar::<()>();
transcript.squeeze_challenge_scalar::<()>();
transcript.read_point().unwrap();
transcript.read_point().unwrap();
transcript.read_point().unwrap();
transcript.read_point().unwrap();
transcript.read_point().unwrap();
transcript.squeeze_challenge_scalar::<()>();
transcript.read_point().unwrap();
transcript.read_point().unwrap();
transcript.read_point().unwrap();
transcript.read_point().unwrap();
transcript.read_point().unwrap();
// Read the challenge x from transcript
let x = transcript.squeeze_challenge().get_scalar();
transcript.read_scalar().unwrap();
// Read second column's eval l(x) from proof
let eval = transcript.read_scalar().unwrap();
points.push(x);
evals.push(eval);
}
// Add one more point/eval pair
// The order is 64, so we need 65 pairs
// In this colum, l(\omega^0) = 0
points.push(Fr::one());
evals.push(Fr::zero());
// Evaluate the polynomial by lagrange interpolation
let poly = lagrange_interpolate(&points, &evals);
let omega = vk.get_domain().get_omega();
// In this colum, l(\omega^2) = l(\omega^3) = l(\omega^4) = secret
let secret = eval_polynomial(&poly, omega.pow([2]));
let secret_commitment = poseidon_base::primitives::Hash::<
_,
P128Pow5T3Compact<Fr>,
ConstantLength<2>,
WIDTH,
RATE,
> ::init()
.hash([secret, Fr::from(0u64)]);
for i in 0..64 {
let (_, _, commitment) = from_serialized(i);
assert_eq!(secret_commitment, commitment);
}
/* End of attack */
}
5. 参考资料
[1] Plonk https://eprint.iacr.org/2019/953.pdf
