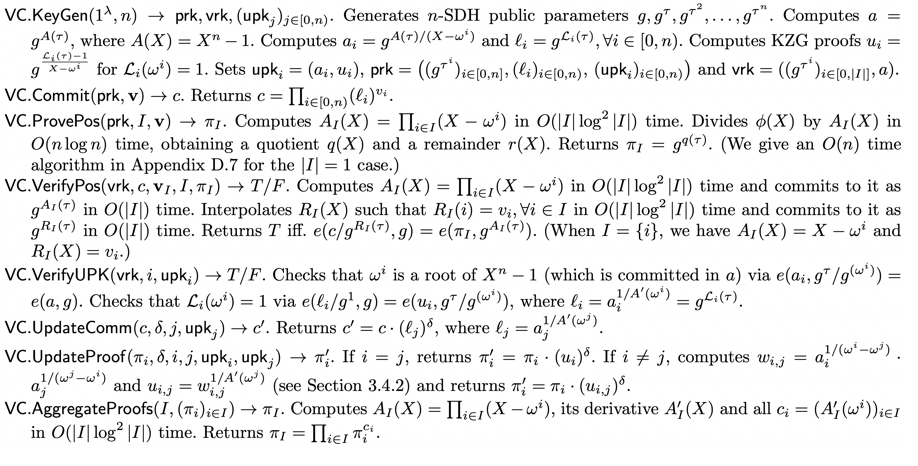🐥 【笔记】An aggregatable subvector commitment(aSVC) scheme

论文地址：Aggregatable Subvector Commitments

aSVC(aggregatable subvector commitment) 是向量承诺（vector commitment）的一种，它可以用来将多个证明聚合成一个小的 subvector 证明。由于aSVC非常低的通信量和计算量，以及它的聚合验证能力，可以使用它来做 payments-only stateless cryptocurrenc。

1. 前提知识

aSVC也是基于KZG10实现的，KZG10的优势在于constant-sized，它的证明的大小和证明的验证时间都是常数规模的。

1.1 KZG10 步骤（单点）

  1. 首先，证明者（prover）和验证者（verifier）获得一组安全的 SRS 公开参数 $(g^{\tau^i})_{i \in [0, n]}$
  2. 证明者（prover）使用 SRS 参数生成 C(x) 的承诺（commitment）, 并公开承诺值 $C = \prod_{i=0}^d (g^{\tau^i})^{c_i} = g^{\phi(\tau)}$
  3. 验证者（verifier）生成随机数 $a$ 并发送给证明者（prover）
  4. 证明者（prover）计算多项式 C(x) 在$a$ 处的取值 $y = C(a)$，并生成证明 $\pi$，将 $(y, \pi)$ 发送给验证者（verifier）。 $\frac{C(\tau)-y}{\tau-a} = q(\tau), \pi = [q(\tau)]_1$，
  5. 验证者（verifier）执行验证 $e(C-[y]_1, [1]_2) = e(\pi, [\tau]_2 - [a]_2)$

1.2 KZG10 步骤（多点）

  1. 首先，证明者（prover）和验证者（verifier）获得一组安全的 SRS 公开参数 $(g^{\tau^i})_{i \in [0, n]}$
  2. 证明者（prover）使用 SRS 参数生成 C(x) 的承诺（commitment）, 并公开承诺值 $C = \prod_{i=0}^d (g^{\tau^i})^{c_i} = g^{\phi(\tau)}$
  3. 验证者（verifier）生成一组挑战数集合 $I$ 并发送给证明者（prover）
  4. 证明者（prover）计算多项式：
    1. $a(x) = \prod_{i \in I} (x-i)$
    2. $r(x) = \sum_{i=1}^m y_i \tau_i(x)$，其中 $y_i = \phi(i), i \in l$, $r(i) = y_i$
    3. 证明者（prover）继续计算证明 $q(x) = \frac{\phi(x) - r(x)}{a(x)}$, $\pi = [q(\tau)]_1$
  5. 证明者（prover）发送 ${ \pi, r(x)}$ 给验证者（verifier）
  6. 验证者（verifier）执行验证： $e(C-[r(\tau)]_1, [1]_2) = e(\pi, [a(\tau)]_2)$

2. 使用KZG10来构造vector commitment

假设有一组值 $\vec{v} = \{ v_i \}_{i \in [0, n)}$，并用它构造向量 $\vec{c}$。 可以使用向量 $\vec{v}$ 构造一个多项式 $\phi(x) = \sum_{i \in [0, n)} L_i(x) v_i$，其中 $L_i(x) = \prod_{j \in [0, n), j \neq i}\frac{x - \omega_i}{\omega_i - \omega_j}$ 为拉格朗日多项式。 当 $x = \omega_i$ 时，$L_i(\omega_i) = 1$，当 $x = \omega_j, j \in [0, n), j \neq i$，，$L_i(\omega_j) = 0$。

到此我们可以利用KZG10的来生成承诺，生成证明和验证证明（可以用来证明一个或多个点）。

  1. $VC.Commit(prk, \vec{v}) \rightarrow c$：证明者（prover）使用 SRS 参数生成 C(x) 的承诺（commitment）, 并公开承诺值 $c = \prod_{i=0}^d (g^{\tau^i})^{c_i} = g^{\phi(\tau)}$。（注意这里需要使用FFT将多项式从点值式转换到系数式，再做承诺）
  2. $VC.ProvePos(prk, I, \vec{v}) \rightarrow \pi_I$：若要验证一个子集 $I \subseteq [0, n)$ 位置的取值 $\vec{v_I} = { v_i}_{i \in I}$。并生成子集I的点的证明：
    1. 计算 $a(x) = \prod_{i \in I} (x-i)$
    2. 计算$r(x) = \sum_{i=1}^m v_i \tau_i(x)$，其中 $y_i = \phi(i), i \in l$, $r(i) = v_i$
    3. 证明者（prover）继续计算证明 $q(x) = \frac{\phi(x) - r(x)}{a(x)}$, $\pi_I = [q(\tau)]_1$
  3. $VC.VerifyPos(vrk, c, \vec{v_I}, I, \pi_I)$: 执行验证： $e(C-[r(\tau)]_1, [1]_2) = e(\pi, [a(\tau)]_2)$

3. 更新承诺和证明

上一节说到如何利用KZG10方案做subvector commitment。当向量中的某个值要被更新后，例如第j个值增加$\delta$，即$v_j’ = v_j + \delta$。 更新后，多项式也会发生变化： $$\phi(x) = \sum_{i \in [0, n)} L_i(x) v_i \rightarrow \phi(x)’ = \sum_{i \in [0, n), i \neq j} L_i(x) v_i + L_j(x) v_j’ = \phi(x) + L_j(x) (v_j’ - v_j) = \phi(x) + L_j(x) \delta $$ $VC.UpdateComm(c, \delta, j, upk_j) \rightarrow T/F$：很显然，在向量中的某个值被更新后，不必重新生成承诺，可以在原来的承诺上直接做更新。 $$ c’ = c + [L_j(\tau)]^\delta $$ 其中 $[L_j(\tau)]$ 可以在初始阶段就生成。

$VC.UpdateProof(\pi_i, \delta, i, j, upk_i, upk_j) \rightarrow \pi_i’$: 我们再来看一下如何更新第i个点的证明，这里分成两种情况：

  1. 当 $j = i$，生成的新证明为： $q’(x) = \frac{\phi’(x) - v_i’}{x-\omega^i}$，其中 $\phi’(x) = \phi(x) + L_j(x) \delta$，$v_i’ = v_i +\delta$ 因此 $q’(x) = \frac{\phi(x) + L_j(x) \delta - v_i +\delta}{x -\omega^i} = q(x) + \frac{(L_j(x) - 1) \delta}{x - \omega^i}$ $\pi_i’ = \pi_i + [\frac{(L_j(\tau) - 1)}{\tau-\omega^i}]^ \delta = \pi_i + u_{i}^\delta$
  2. 当 $j \neq i$，生成的新证明为： $q’(x) = \frac{\phi’(x) - v_i}{x-\omega^i} =q(x) + \frac{L_j(x) \delta}{x-\omega^i}$， $\pi_i’ = \pi_i + [\frac{L_j(\tau)}{\tau-\omega^i}]^\delta = \pi_i + u_{ij}^\delta$ 其中 $u_{ij}, u_{i}$ 可以在初始阶段就生成。

4. partial fraction decomposition

多项式 $\phi(x) = \sum_{i \in [0, n)} L_i(x) v_i$，其中 $L_i(x) = \prod_{j \in [0, n), j \neq i}\frac{x - \omega_i}{\omega_i - \omega_j}$ 为拉格朗日多项式，我们可以使用 partial fraction decomposition 来变换$L_i(x)$。 首先来定义多项式 $A_I(x) = \prod_{i \in I}(x - \omega^i)$（令 $A(x) = \prod_{i \in [0, n)}(x - \omega^i)$）。对多项式 $A_I(x)$ 求导， $$ A_I’(x) = \prod_{i\in I, i \in i_0} (x - \omega^i) + \prod_{i\in I, i \in i_1} (x - \omega^i) + …+ \prod_{i\in I, i \in i_{m-1}} (x - \omega^i) = \sum_{j \in I}(\prod_{i\in I, i \neq j} (x - \omega^i)) = \sum_{j \in I} \frac{A_I(x)}{x - \omega^j} $$ 那么 $A_I’(\omega^i) = \sum_{j \in I} \frac{A_I(\omega^i)}{\omega^i - \omega^j} = 0 + …+ \frac{A_I(\omega^i)}{\omega^i - \omega^i} + ..+ 0 = \prod_{j \in I, i \neq j}(\omega^i - \omega^j)$

我们还可以化简 $L_i(x)$： $$ L_i(x) = \prod_{j \in [0, n), j \neq i}\frac{x - \omega_i}{\omega_i - \omega_j} = \prod_{j \in [0, n), j \neq i} (x-\omega^i) \cdot \frac{1}{\prod_{j \in [0, n), j \neq i} (\omega_i - \omega_j)} = \frac{A(x)}{x-\omega^i} \cdot \frac{1}{A’(\omega^i)} $$ 及 $\tau_i(x) = \frac{A_I(x)}{A’_I(x)(x -\omega^i)}$ 另外，对于$A(x)$来说，还满足$A(x) = x^n -1, A’(x) = n x^{n-1}$。 $\phi(x) = \sum_{i \in [0, n)} L_i(x) v_i = A(x) \sum_{i \in [0, n)} \frac{v_i}{A’(\omega^i) (x-\omega^i)}$

有一种特殊情况，当$r(x) = 1$恒成立时，说明 $v_i =1$。那么 $\phi(x) = A(x) \sum_{i \in I} \frac{1}{A’(\omega^i) (x-\omega^i)} =1$也必然成立，那么 $\frac{1}{A_I(x)} = \sum_{i \in I} \frac{1}{A’(\omega^i) (x-\omega^i)}$。

5. 聚合证明

$VC.AggregateProofs(I, (\pi_i)_{i \in I}) \rightarrow \pi_I$ KZG10可以做单个点的证明，也可以正多个点的batch证明。我们可以把多个单点的证明聚合成一个batch证明。 已知一组点$I$的证明 $\{ \pi_i\}_{i \in I}$，其中 $\pi_i = \frac{\phi(\tau) - v_i}{\tau - \omega^i}$ 而这组点$I$ 的聚合证明 $\pi = [\frac{\phi(\tau) - r(x)}{A_I(x)}]$，其中 $A_I(x) = \prod_{i \in I} (x-i)$， $r(x) = \sum_{i=1}^m v_i \tau_i(x)$。

$q(x) =\frac{\phi(x) - r(x)}{A_I(x)} = \phi(x)\sum_{j \in I}\frac{1}{A_I’(\omega^j) (x -\omega^j)} - \frac{\sum_{j \in I}\frac{A_I(x)}{A’_I(\omega^j)(x -\omega^i)} v_i}{A_I(x)}$

$=\sum_{j \in I}\frac{\phi(x)}{A_I’(\omega^j) (x -\omega^j)} - \sum_{j \in I}\frac{v_i}{A’_I(\omega^j)(x -\omega^i)} =\sum_{j \in I}\frac{\phi(x) - v_i}{A_I’(\omega^j) (x -\omega^j)}$

$= \sum_{j \in I}\frac{q_i(x)}{A_I’(\omega^j)}$ 其中 $A_I’(\omega^j)$ 可以在初始阶段就生成。

6. KeyGen 及验证

除了最初的一组安全的 SRS 公开参数 $(g^{\tau^i})_{i \in [0, n]}$，aSVC在处理承诺和证明之前，还需要生成一系列的KEY，以提高承诺和证明速度。

  1. $VC.KeyGen(1^\lambda, n) \rightarrow prk, vrk, (upk_j)_{j \in [0, n)}$：
    1. 计算 $a = g^{A(\tau)} = g^{\tau^n-1}$
    2. 计算 ${a_i = g^{\frac{A(\tau)}{x- \omega^i}}}_{i \in [0, n)}$
    3. 计算${l_i = g^{L_i(\tau)}}_{i \in [0,n)} = a_i^{\frac{1}{A’(\omega^i)}}$
    4. 计算 ${u_i = g^{\frac{L_i(\tau)-1}{x - \omega^i}}}_{i \in [0,n)} = a_i^{\frac{1}{A’(\omega^i)}}$
    5. 构造 $upk_i = (a_i, u_i)$
    6. 构造 $prk = ((g^\tau)_{i \in [0, n)}, (l_i)_{i \in [0, n)}, (upk_i)_{i \in [0, n)})$
    7. 构造 $vrk = ((g^\tau)_{i \in [0, n)}, a)$
  2. $VC.VerifyUPK(vrk, i, upk_i) \rightarrow T/F$:
    1. 为了验证 $\omega^i$ 是 $x^n-1$ 的根，可以通过 $e(a_i, [\tau -\omega^i) = e(a, g)$
    2. 为了验证 $L_i(\omega^i)=1$，$e(l_i - [1], [1]) = e(u_i, [\tau] - [\omega^i])$

7. 完整的验证步骤

asvc

Even Lu

<< Previous post

【笔记】Sumcheck

Next post >>

【笔记】A Folding Scheme for Committed Relaxed R1CS